常用数据结构与算法,大厂笔试刷题记录。
一、数组 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
1 2 3 4 5 6 7 8 9 10 public int maxSubArray (int [] nums) { int res = nums[0 ]; for (int i = 1 ; i < nums.length; i++) { nums[i] += Math.max(nums[i - 1 ], 0 ); res = Math.max(res, nums[i]); } return res; }
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target两个 整数,并返回它们的数组下标。
1 2 3 4 5 6 7 8 9 10 11 12 public int [] twoSum(int [] nums, int target) { Map<Integer,Integer> map=new HashMap <>(); for (int i=0 ;i<nums.length;i++){ if (map.containsKey(target-nums[i])){ return new int []{i,map.get(target-nums[i])}; } map.put(nums[i],i); } return new int [0 ]; }
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
1 2 3 4 5 6 7 8 9 public void merge (int [] nums1, int m, int [] nums2, int n) { int len = m + n - 1 ; int len1 = m - 1 , len2 = n - 1 ; while (len1 >= 0 && len2 >= 0 ) { nums1[len--] = nums1[len1] > nums2[len2] ? nums1[len1--] : nums2[len2--]; } System.arraycopy(nums2, 0 , nums1, 0 , len2 + 1 ); }
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public int search (int [] nums, int target) { int i = 0 , j = nums.length - 1 ; while (i <= j) { int mid = i + (j - i) / 2 ; if (nums[mid] < target) { i = mid + 1 ; } else if (nums[mid] > target) { j = mid - 1 ; } else { return mid; } } return -1 ; }
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
1 2 3 4 5 6 7 8 9 10 11 public void moveZeroes (int [] nums) { int j = 0 ; for (int i = 0 ; i < nums.length; i++) { if (nums[i] != 0 ) { nums[j++] = nums[i]; } } while (j < nums.length) { nums[j++] = 0 ; } }
给你一个 非严格递增排列 的数组 nums ,请你** 原地 ** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
1 2 3 4 5 6 7 8 9 10 11 12 public int removeDuplicates (int [] nums) { if (nums.length == 0 ) { return 0 ; } int index = 0 ; for (int i = 1 ; i < nums.length; i++) { if (nums[i] != nums[index]) { nums[++index] = nums[i]; } } return index + 1 ; }
从 0 号成员起开始计数,排在第 target 位的成员离开圆桌,且成员离开后从下一个成员开始计数。请返回游戏结束时最后一位成员的编号。
1 2 3 4 5 6 7 8 9 10 11 12 13 public int lastRemaining (int n, int m) { List<Integer> list = new ArrayList <>(n); for (int i = 0 ; i < n; i++) { list.add(i); } int idx = 0 ; while (n > 1 ) { idx = (idx + m - 1 ) % n; list.remove(idx); n--; } return list.get(0 ); }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public int [] exchange(int [] nums) { int i = 0 , j = nums.length - 1 ; while (i < j) { while (i < j && nums[i] % 2 == 1 ) { i++; } while (i < j && nums[j] % 2 == 0 ) { j--; } int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } return nums; }
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public List<List<Integer>> threeSum (int [] nums) { List<List<Integer>> res = new ArrayList <>(); Arrays.sort(nums); for (int i = 0 ; i < nums.length - 2 ; i++) { if (i > 0 && nums[i] == nums[i - 1 ]) { continue ; } int left = i + 1 ; int right = nums.length - 1 ; while (left < right) { int sum = nums[i] + nums[left] + nums[right]; if (sum == 0 ) { res.add(Arrays.asList(nums[i], nums[left], nums[right])); while (left < right && nums[left] == nums[left + 1 ]) { left++; } while (left < right && nums[right] == nums[right - 1 ]) { right--; } left++; right--; } else if (sum < 0 ) { left++; } else { right--; } } } return res; }
手撕快速排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public void quickSort (int [] nums, int low, int high) { if (low < high) { int pivotIndex = partition(nums, low, high); quickSort(nums, low, pivotIndex - 1 ); quickSort(nums, pivotIndex + 1 , high); } } private int partition (int [] nums, int low, int high) { int pivot = nums[high]; int i = low - 1 ; for (int j = low; j < high; j++) { if (nums[j] < pivot) { i++; swap(nums, i, j); } } swap(nums, i + 1 , high); return i + 1 ; } private void swap (int [] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; }
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int [][] merge(int [][] intervals) { if (intervals==null ||intervals.length<=1 ){ return intervals; } Arrays.sort(intervals,(a,b)->Integer.compare(a[0 ],b[0 ])); List<int []> merged=new ArrayList <>(); int [] currentInterval=intervals[0 ]; for (int i = 1 ; i < intervals.length; i++) { if (intervals[i][0 ]<=currentInterval[1 ]){ currentInterval[1 ]=Math.max(currentInterval[1 ],intervals[i][1 ]); }else { merged.add(currentInterval); currentInterval=intervals[i]; } } merged.add(currentInterval); return merged.toArray(new int [merged.size()][]); }
12、在排序数组中查找元素的左右边界 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 public int [] searchRange(int [] nums, int target) { int [] result = {-1 , -1 }; int first = findFirst(nums, target); if (first == -1 ) { return result; } int last = findLast(nums, target); result[0 ] = first; result[1 ] = last; return result; } private int findFirst (int [] nums, int target) { int left = 0 ; int right = nums.length - 1 ; int first = -1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] >= target) { right = mid - 1 ; if (nums[mid] == target) { first = mid; } } else { left = mid + 1 ; } } return first; } private int findLast (int [] nums, int target) { int left = 0 ; int right = nums.length - 1 ; int last = -1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] <= target) { left = mid + 1 ; if (nums[mid] == target) { last = mid; } } else { right = mid - 1 ; } } return last; }
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 1. 从右到左遍历给定的排列,找到第一个破坏升序的相邻元素对,记为i-1 和i。即找到满足nums[i-1 ] < nums[i]的i值。 2. 如果找不到这样的相邻元素对,说明给定排列已经是字典序最大的排列,将其翻转为最小排列即可。 3. 如果找到了相邻元素对,从右到左找到第一个大于nums[i-1 ]的元素,记为j。 4. 交换nums[i-1 ]和nums[j]。 5. 将从i开始到最右边的元素进行翻转,以得到下一个字典序更大的排列。 public void nextPermutation (int [] nums) { int i = nums.length - 2 ; while (i >= 0 && nums[i] >= nums[i + 1 ]) { i--; } if (i >= 0 ) { int j = nums.length - 1 ; while (j >= 0 && nums[j] <= nums[i]) { j--; } swap(nums, i, j); } reverse(nums, i + 1 ); } private void swap (int [] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } private void reverse (int [] nums, int start) { int i = start; int j = nums.length - 1 ; while (i < j) { swap(nums, i, j); i++; j--; } }
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
子数组 是数组的连续子序列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int maxProduct (int [] nums) { int maxProduct = nums[0 ]; int currentMax = nums[0 ]; int currentMin = nums[0 ]; for (int i = 1 ; i < nums.length; i++) { if (nums[i] < 0 ) { int temp = currentMax; currentMax = currentMin; currentMin = temp; } currentMax = Math.max(nums[i], currentMax * nums[i]); currentMin = Math.min(nums[i], currentMin * nums[i]); maxProduct = Math.max(maxProduct, currentMax); } return maxProduct; }
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数。
前缀和是一种常用于解决数组或序列问题的技巧,它通常用于快速计算某个区间内元素的和。前缀和的基本思想是将原数组的前缀和(或累积和)存储在一个辅助数组中,以便在常数时间内获取任意区间的和。
下面是前缀和的基本概念:
前缀和数组 :前缀和数组是一个与原始数组具有相同长度的数组,其中每个元素存储了原始数组从开头到当前位置的所有元素的累积和。通常,前缀和数组的第一个元素为0,然后依次计算后续元素的值。
计算前缀和数组 :计算前缀和数组的一种常见方法是使用迭代。从数组的第一个元素开始,依次计算前缀和数组中的每个元素。例如,如果原数组为nums,前缀和数组prefixSum可以如下计算:
1 2 3 4 prefixSum[0 ] = 0 ; for (int i = 1 ; i < nums.length; i++) { prefixSum[i] = prefixSum[i - 1 ] + nums[i]; }
计算区间和 :一旦有了前缀和数组,你可以用它来快速计算任意区间 [i, j] 内元素的和,其中 i 和 j 是数组的索引。区间 [i, j] 的和等于 prefixSum[j] - prefixSum[i - 1]。需要注意,如果 i 等于0,那么 prefixSum[i - 1] 通常被定义为0。
通过遍历数组并计算累积和,同时使用哈希表来记录每个前缀和出现的次数。当找到一个前缀和与当前和的差值等于k时,就说明存在一个子数组的和等于k,因此增加计数器count。最后返回count即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public int subarraySum (int [] nums, int k) { int count = 0 ; int sum = 0 ; HashMap<Integer, Integer> map = new HashMap <>(); map.put(0 , 1 ); for (int i = 0 ; i < nums.length; i++) { sum += nums[i]; if (map.containsKey(sum - k)) { count += map.get(sum - k); } map.put(sum, map.getOrDefault(sum, 0 ) + 1 ); } return count; }
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数 ,如果不存在,返回0。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public int minSubArrayLen (int target, int [] nums) { int left = 0 , right = 0 ; int sum = 0 ; int count = Integer.MAX_VALUE; while (right < nums.length) { sum += nums[right]; while (sum >= target) { count = Math.min(count, right - left + 1 ); sum -= nums[left]; left++; } right++; } return count == Integer.MAX_VALUE ? 0 : count; }
17、三数排序 存在数组[1,0,0,0,2,0,1,2],重新排序,使得按0,1,2排序。同leetcode荷兰三色旗问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public void sortColors (int [] nums) { int low = 0 , mid = 0 , high = nums.length - 1 ; while (mid <= high) { if (nums[mid] == 0 ) { swap(nums, low++, mid++); } else if (nums[mid] == 2 ) { swap(nums, mid, high--); } else { mid++; } } } private void swap (int [] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; }
18、旋转数组查找 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 public static int rotatedBinarySearch (int [] array, int target) { if (nums == null || nums.length == 0 ) { return -1 ; } int left = 0 , right = nums.length - 1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] == target) { return mid; } if (nums[left] <= nums[mid]) { if (target >= nums[left] && target < nums[mid]) { right = mid - 1 ; } else { left = mid + 1 ; } } else { if (target > nums[mid] && target <= nums[right]) { left = mid + 1 ; } else { right = mid - 1 ; } } } return -1 ; } }
二、字符串 给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public String addStrings (String num1, String num2) { StringBuilder res = new StringBuilder (); int m = num1.length() - 1 , n = num2.length() - 1 ; int carry = 0 ; while (m >= 0 || n >= 0 ) { int n1 = m >= 0 ? num1.charAt(m) - '0' : 0 ; int n2 = n >= 0 ? num2.charAt(n) - '0' : 0 ; int ans = n1 + n2 + carry; carry = ans / 10 ; res.append(ans % 10 ); m--; n--; } if (carry == 1 ) { res.append(carry); } return res.reverse().toString(); }
编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀,返回空字符串 ""。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public String longestCommonPrefix (String[] strs) { if (strs == null || strs.length == 0 ) { return "" ; } String prefix = strs[0 ]; for (String s : strs) { while (s.indexOf(prefix) != 0 ) { prefix = prefix.substring(0 , prefix.length() - 1 ); if (prefix.isEmpty()) { return "" ; } } } return prefix; }
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
解题记录:
1、移除重复元素时,可能存在多个连续的重复元素,需要使用while语句。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public int lengthOfLongestSubstring (String s) { int maxLength = 0 ; int left = 0 , right = 0 ; Set<Character> set = new HashSet <>(); while (right < s.length()) { if (!set.contains(s.charAt(right))) { set.add(s.charAt(right)); maxLength = Math.max(maxLength, right - left + 1 ); right++; } else { set.remove(s.charAt(left)); left++; } } return maxLength; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 // 2、输出具体子串 public static String findLongestSubstring(String s) { if (s == null || s.isEmpty()) { return ""; } int start = 0; // 子串起始位置 int maxLen = 0; // 最大长度 int maxStart = 0; // 最长子串的起始位置 HashMap<Character, Integer> charIndexMap = new HashMap<>(); // 记录字符及其最近一次出现的位置 for (int i = 0; i < s.length(); i++) { char ch = s.charAt(i); // 如果字符已经在窗口内,移动左边界 if (charIndexMap.containsKey(ch) && charIndexMap.get(ch) >= start) { start = charIndexMap.get(ch) + 1; } // 更新字符的最新位置 charIndexMap.put(ch, i); // 检查当前窗口是否是最长的 if (i - start + 1 > maxLen) { maxLen = i - start + 1; maxStart = start; } } // 返回最长子串 return s.substring(maxStart, maxStart + maxLen); }
给你一个字符串 s,找到 s 中最长的回文子串。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public String getLongestPalinedromeString (String s) { String res = "" ; for (int i = 0 ; i < s.length(); i++) { String s1 = palinedrome(s, i, i); String s2 = palinedrome(s, i, i + 1 ); res = res.length() > s1.length() ? res : s1; res = res.length() > s2.length() ? res : s2; } return res; } private String palinedrome (String s,int i,int j) { while (i >= 0 && j < s.length() && s.charAt(i) == s.charAt(j)) { i--; j++; } return s.substring(i+1 ,j); }
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public String multiply (String num1, String num2) { int m = num1.length(), n = num2.length(); int [] res = new int [m + n]; for (int i = m - 1 ; i >= 0 ; i--) { for (int j = n - 1 ; j >= 0 ; j--) { int mul = (num1.charAt(i) - '0' ) * (num2.charAt(j) - '0' ); int p1 = i + j; int p2 = i + j + 1 ; int sum = mul + res[p2]; res[p1] += sum / 10 ; res[p2] = sum % 10 ; } } StringBuilder str = new StringBuilder (); for (int i = 0 ; i < res.length; i++) { if (i == 0 && res[i] == 0 ) { continue ; } str.append(res[i]); } return str.toString(); }
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int countSubstrings (String s) { int count = 0 ; for (int i = 0 ; i < s.length(); i++) { count += expandAroundCenter(s, i, i); count += expandAroundCenter(s, i, i + 1 ); } return count; } private int expandAroundCenter (String s, int left, int right) { int count = 0 ; while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) { count++; left--; right++; } return count; }
三、栈 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public boolean isValid (String s) { if (s.length()%2 ==1 ){ return false ; } Map<Character,Character> map=new HashMap <>(); map.put(')' ,'(' ); map.put(']' ,'[' ); map.put('}' ,'{' ); Deque<Character> stack=new LinkedList <>(); for (int i = 0 ; i < s.length(); i++) { char c=s.charAt(i); if (map.containsKey(c)){ if (stack.isEmpty()||stack.peek()!=map.get(c)){ return false ; } stack.pop(); }else { stack.push(c); } } return stack.isEmpty(); }
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class MyQueue { Stack<Integer> stack1; Stack<Integer> stack2; public MyQueue () { stack1 = new Stack <>(); stack2 = new Stack <>(); } public void push (int x) { stack1.push(x); } public int pop () { if (stack2.isEmpty()) { while (!stack1.isEmpty()) { stack2.push(stack1.pop()); } } return stack2.pop(); } public int peek () { if (stack2.isEmpty()){ while (!stack1.isEmpty()) { stack2.push(stack1.pop()); } } return stack2.peek(); } public boolean empty () { return stack1.isEmpty() && stack2.isEmpty(); } }
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。int getMin() 获取堆栈中的最小元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class MinStack { Stack<Integer> stack1; Stack<Integer> stack2; public MinStack () { stack1=new Stack <>(); stack2=new Stack <>(); } public void push (int val) { stack1.push(val); if (stack2.isEmpty() || stack2.peek() >= val) { stack2.push(val); } } public void pop () { if (stack2.peek().equals(stack1.pop())){ stack2.pop(); } } public int top () { return stack1.peek(); } public int getMin () { return stack2.peek(); } }
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复 ,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
思路:(1)遍历入栈数组,并将其放入栈中;(2)栈不空,循环判断栈顶元素是否和出栈数组第一个元素相同,相同则出栈,并将指向出栈数组的索引+1;(3)最后判断栈是否为空,空则为合法出栈序列。
1 2 3 4 5 6 7 8 9 10 11 12 public boolean validateStackSequences (int [] pushed, int [] popped) { Stack<Integer> stack=new Stack <>(); int i=0 ; for (int c:pushed){ stack.push(c); while (!stack.isEmpty()&&stack.peek()==popped[i]){ stack.pop(); i++; } } return stack.isEmpty(); }
给定一个经过编码的字符串,返回它解码后的字符串。
输入:s = “3[a2[c]]”
输入:s = “2[abc]3[cd]ef”
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 public String decodeString (String s) { Stack<Integer> countStack = new Stack <>(); Stack<String> strStack = new Stack <>(); StringBuilder res = new StringBuilder (); int index = 0 ; while (index < s.length()) { char c = s.charAt(index); if (Character.isDigit(c)) { int count = 0 ; while (Character.isDigit(s.charAt(index))) { count = count * 10 + (s.charAt(index) - '0' ); index++; } countStack.push(count); } else if (c == '[' ) { strStack.push(res.toString()); res.setLength(0 ); index++; } else if (c == ']' ) { StringBuilder temp = new StringBuilder (strStack.pop()); int repeatTimes = countStack.pop(); for (int i = 0 ; i < repeatTimes; i++) { temp.append(res); } res = temp; index++; } else { res.append(c); index++; } } return res.toString(); }
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
思路:辅助栈存储数组下标
(1)遍历温度数组,入栈,并循环判断“栈不空,且当前数组元素是否大于栈顶元素,得到栈中元素到下一个更大元素的下标步长,即i-stack.pop()。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public int [] dailyTemperatures(int [] T) { int [] result = new int [T.length]; Stack<Integer> stack = new Stack <>(); for (int i = 0 ; i < T.length; i++) { while (!stack.isEmpty() && T[i] > T[stack.peek()]) { int index = stack.pop(); result[index] = i - index; } stack.push(i); } return result; }
7、接雨水
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public int trap (int [] height) { if (height==null ){ return 0 ; } Stack<Integer> stack=new Stack <>(); int ans=0 ; for (int i=0 ;i<height.length;i++){ while (!stack.isEmpty()&&height[stack.peek()]<height[i]){ int curIdx=stack.pop(); while (!stack.isEmpty()&&height[stack.peek()]==height[curIdx]){ stack.pop(); } if (!stack.isEmpty()){ int stackTop=stack.peek(); ans += (Math.min(height[stackTop], height[i]) - height[curIdx]) * (i - stackTop - 1 ); } } stack.add(i); } return ans; }
四、链表 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
1 2 3 4 5 6 7 8 9 10 11 public ListNode reverseList (ListNode head) { ListNode pre=null ; ListNode cur=head; while (cur!=null ){ ListNode temp=cur.next; cur.next=pre; pre=cur; cur=temp; } return pre; }
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public ListNode mergeTwoLists (ListNode list1, ListNode list2) { ListNode mergeList = new ListNode (-1 ); ListNode cur=mergeList; while (list1 != null && list2 != null ) { if (list1.val < list2.val) { cur.next = list1; list1 = list1.next; } else { cur.next = list2; list2 = list2.next; } cur = cur.next; } cur.next = list1 != null ? list1 : list2; return mergeList.next; }
给你一个链表的头节点 head ,判断链表中是否有环。
1 2 3 4 5 6 7 8 9 10 11 12 public boolean hasCycle (ListNode head) { ListNode fast = head, slow = head; while (fast != null && fast.next != null ) { fast = fast.next.next; slow = slow.next; if (fast == slow) { return true ; } } return false ; }
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
1 2 3 4 5 6 7 8 public ListNode getIntersectionNode (ListNode headA, ListNode headB) { ListNode first = headA, second = headB; while (first != second) { first = first != null ? first.next : headB; second = second != null ? second.next : headA; } return first; }
获取链表中倒数第k个结点。
1 2 3 4 5 6 7 8 9 10 11 public ListNode kthReverseNode (ListNode head, int k) { ListNode fast = head, slow = head; while (k-- != 0 ) { fast = fast.next; } while (fast != null ) { fast = fast.next; slow = slow.next; } return slow; }
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则返回 false 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public boolean isPalindrome (ListNode head) { if (head == null || head.next == null ) { return true ; } ListNode fast = head, slow = head; ListNode cur = head, pre = null ; while (fast != null && fast.next != null ) { cur = slow; fast = fast.next.next; slow = slow.next; cur.next = pre; pre = cur; } if (fast != null ) { slow = slow.next; } while (slow != null && pre != null ) { if (slow.val != pre.val) { return false ; } slow = slow.next; pre = pre.next; } return true ; }
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
1 2 3 4 5 6 7 8 9 10 11 public ListNode deleteDuplicates (ListNode head) { ListNode cur = head; while (cur != null && cur.next != null ) { if (cur.val == cur.next.val) { cur.next = cur.next.next; } else { cur = cur.next; } } return head; }
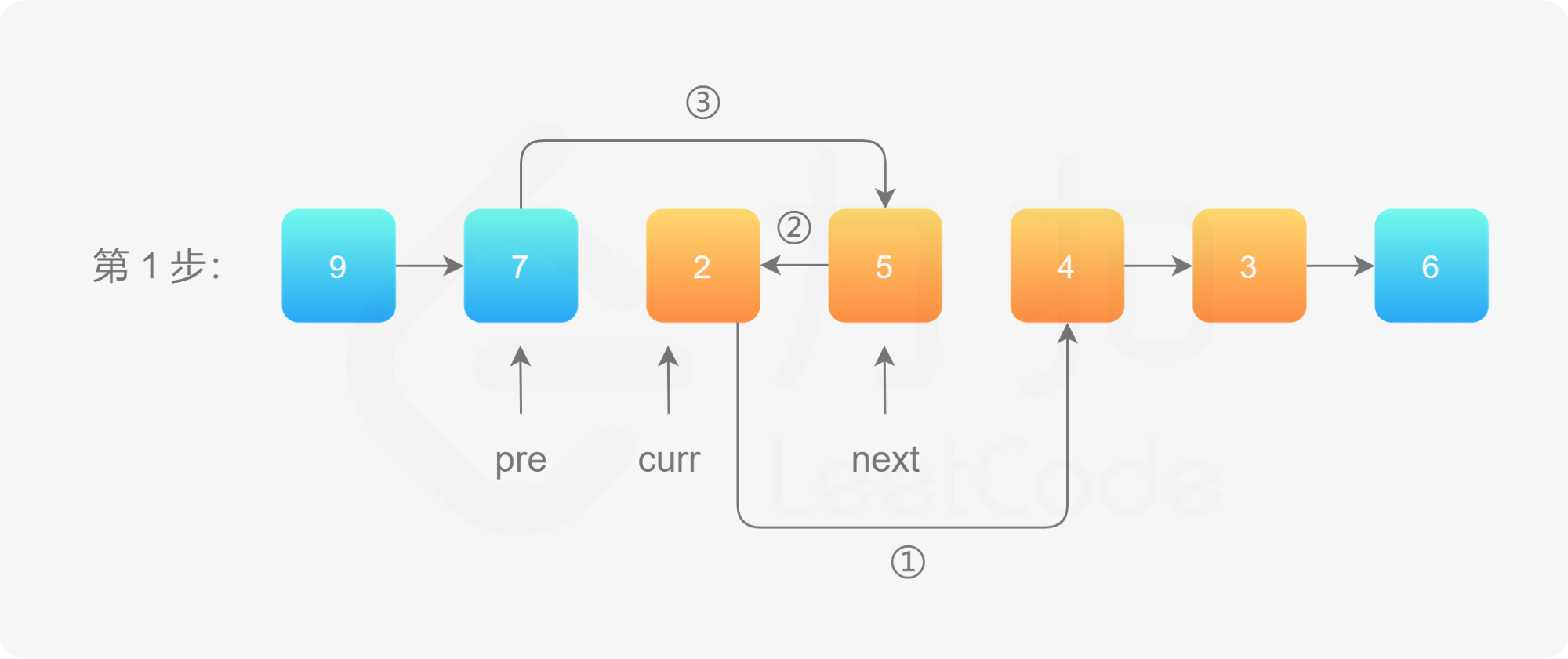
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public ListNode reverseBetween (ListNode head, int left, int right) { ListNode dummy=new ListNode (-1 ); dummy.next=head; ListNode pre=dummy; for (int i=1 ;i<left;i++){ pre=pre.next; } ListNode cur=pre.next; for (int i=left;i<right;i++){ ListNode node=cur.next; cur.next=node.next; node.next=pre.next; pre.next=node; } return dummy.next; }
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public ListNode detectCycle (ListNode head) { ListNode fast = head, slow = head; while (fast != null && fast.next != null ) { fast=fast.next.next; slow=slow.next; if (fast == slow) { ListNode index1 = fast; ListNode index2 = head; while (index1 != index2) { index1 = index1.next; index2 = index2.next; } return index1; } } return null ; }
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
1 L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
1 L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 public void reorderList (ListNode head) { if (head == null ) { return ; } ListNode mid = findMid(head); ListNode head2=mid.next; mid.next=null ; head2=reverse(head2); ListNode head1=head; mergeLists(head1,head2); } private void mergeLists (ListNode head1, ListNode head2) { while (head1 != null && head2 != null ) { ListNode temp1 = head1.next; ListNode temp2 = head2.next; head1.next = head2; head1 = temp1; head2.next = head1; head2 = temp2; } } private ListNode findMid (ListNode head) { ListNode fast = head, slow = head; while (fast != null && fast.next != null ) { fast = fast.next.next; slow = slow.next; } return slow; } private ListNode reverse (ListNode head) { ListNode pre=null ; ListNode cur=head; while (cur!=null ){ ListNode temp=cur.next; cur.next=pre; pre=cur; cur=temp; } return pre; }
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public ListNode sortList (ListNode head) { if (head == null || head.next == null ) { return head; } ListNode slow = head; ListNode fast = head; ListNode pre = null ; while (fast != null && fast.next != null ) { pre = slow; fast = fast.next.next; slow = slow.next; } pre.next = null ; ListNode left = sortList(head); ListNode right = sortList(slow); return merge(left, right); } private ListNode merge (ListNode left, ListNode right) { ListNode dummy = new ListNode (0 ); ListNode cur = dummy; while (left != null && right != null ) { if (left.val < right.val) { cur.next = left; left = left.next; } else { cur.next = right; right = right.next; } cur = cur.next; } cur.next = left == null ? right : left; return dummy.next; }
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
思路:找到第K个节点,翻转前K个节点,然后递归进行K组翻转。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public ListNode reverseKGroup (ListNode head, int k) { if (head == null || head.next == null ) { return head; } ListNode tail = head; for (int i = 0 ; i < k; i++) { if (tail == null ) { return head; } tail = tail.next; } ListNode newHead = reverse(head, tail); head.next = reverseKGroup(tail, k); return newHead; } private ListNode reverse (ListNode head, ListNode tail) { ListNode pre = null ; ListNode cur = head; while (cur != tail) { ListNode temp = cur.next; cur.next = pre; pre = cur; cur = temp; } return pre; }
给定单链表的头节点 head ,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排序的列表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public ListNode oddEvenList (ListNode head) { if (head == null || head.next == null ) { return head; } ListNode odd = head; ListNode even = head.next; ListNode temp = even; while (even != null && even.next != null ) { odd.next = even.next; odd = odd.next; even.next = odd.next; even = even.next; } odd.next = temp; return head; }
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public ListNode rotateRight (ListNode head, int k) { if (head == null || head.next == null || k == 0 ) { return head; } int length = 1 ; ListNode tail = head; while (tail.next != null ) { tail = tail.next; length++; } tail.next = head; int steps = length - k % length; ListNode newTail = tail; while (steps > 0 ) { newTail = newTail.next; head = head.next; steps--; } newTail.next = null ; return head; }
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public ListNode partition (ListNode head, int x) { ListNode smallerHead = new ListNode (0 ); ListNode greaterHead = new ListNode (0 ); ListNode smaller = smallerHead; ListNode greater = greaterHead; while (head != null ) { if (head.val < x) { smaller.next = head; smaller = smaller.next; } else { greater.next = head; greater = greater.next; } head = head.next; } greater.next = null ; smaller.next = greaterHead.next; return smallerHead.next; }
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
2—>4—>6
1—>2—>5
结果: 3—>6—>1—>1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public ListNode addTwoNumbers (ListNode l1, ListNode l2) { ListNode dummy = new ListNode (-1 ); ListNode cur = dummy; int carry = 0 ; while (l1 != null || l2 != null ) { int val1 = l1 == null ? 0 : l1.val; int val2 = l2 == null ? 0 : l2.val; int sum = val1 + val2 + carry; carry = sum / 10 ; cur.next = new ListNode (sum % 10 ); cur = cur.next; if (l1 != null ) { l1 = l1.next; } if (l2 != null ) { l2 = l2.next; } } if (carry == 1 ) { cur.next = new ListNode (1 ); } return dummy.next; }
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。
1 2 3 4 5 6 7 8 9 10 public ListNode swapPairs (ListNode head) { if (head==null ||head.next==null ){ return head; } ListNode temp=head.next; head.next=swapPairs(temp.next); temp.next=head; return temp; }
18、删除链表中的倒数第K个结点 思路:需要定义一个哑结点,如删除第一个元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public ListNode removeNthFromEnd (ListNode head, int n) { ListNode dummy = new ListNode (0 ); dummy.next = head; ListNode fast = dummy, slow = dummy; for (int i = 0 ; i <= n; i++) { fast = fast.next; } while (fast != null ) { fast = fast.next; slow = slow.next; } slow.next = slow.next.next; return dummy.next; }
19、LRU缓存实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 class LRUCache { class Node { int key; int value; Node prev; Node next; public Node(int key, int value) { this.key = key; this.value = value; } } private int capacity; private Map<Integer, Node> cache; private Node head; private Node tail; // HashMap+双链表 public LRUCache(int capacity) { this.capacity = capacity; this.cache = new HashMap<>(); this.head = new Node(0, 0); this.tail = new Node(0, 0); head.next = tail; tail.prev = head; } // get方法根据给定的键获取对应的值,如果存在则返回值,并将该节点移动到链表头部。 public int get(int key) { if (cache.containsKey(key)) { Node node = cache.get(key); removeNode(node); addToHead(node); return node.value; } return -1; } // put方法根据给定的键和值插入或更新缓存中的节点,如果插入操作导致容量超过限制,则逐出最久未使用的节点。 public void put(int key, int value) { if (cache.containsKey(key)) { Node node = cache.get(key); node.value = value; removeNode(node); addToHead(node); } else { if (cache.size() == capacity) { Node tailPrev = tail.prev; removeNode(tailPrev); cache.remove(tailPrev.key); } Node newNode = new Node(key, value); cache.put(key, newNode); addToHead(newNode); } } private void removeNode(Node node) { node.prev.next = node.next; node.next.prev = node.prev; } private void addToHead(Node node) { node.prev = head; node.next = head.next; head.next.prev = node; head.next = node; } }
五、二叉树 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
递归:
1 2 3 4 5 6 7 8 9 10 11 12 13 public List<Integer> inorderTraversal (TreeNode root) { List<Integer> res=new ArrayList <>(); inOrder(root,res); return res; } private void inOrder (TreeNode root, List<Integer> res) { if (root==null ){ return ; } inOrder(root.left,res); res.add(root.val); inOrder(root.right,res); }
迭代:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public List<Integer> inorderTraversalByIterator (TreeNode root) { List<Integer> res=new ArrayList <>(); Deque<TreeNode> stack=new LinkedList <>(); while (root!=null ||!stack.isEmpty()){ while (root!=null ){ stack.push(root); root=root.left; } root=stack.pop(); res.add(root.val); root=root.right; } return res; }
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
递归:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public List<Integer> preorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <Integer>(); preorder(root, result); return result; } public void preorder (TreeNode root, List<Integer> result) { if (root == null ) { return ; } result.add(root.val); preorder(root.left, result); preorder(root.right, result); }
迭代:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public List<Integer> preOrderTraversalByIterator (TreeNode root) { List<Integer> res=new ArrayList <>(); if (root==null ){ return res; } Stack<TreeNode> stack=new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode node=stack.pop(); res.add(node.val); while (node.right!=null ){ stack.push(node.right); } while (node.left!=null ){ stack.push(node.left); } } return res; }
递归:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public List<Integer> postorderTraversal (TreeNode root) { List<Integer> res = new ArrayList <>(); postorder(root, res); return res; } void postorder (TreeNode root, List<Integer> list) { if (root == null ) { return ; } postorder(root.left, list); postorder(root.right, list); list.add(root.val); }
迭代:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public List<Integer> postorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ){ return result; } Stack<TreeNode> stack = new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode node = stack.pop(); result.add(node.val); if (node.left != null ){ stack.push(node.left); } if (node.right != null ){ stack.push(node.right); } } Collections.reverse(result); return result; }
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public static List<List<Integer>> levelOrder (TreeNode root) { List<List<Integer>> result = new ArrayList <>(); if (root == null ) { return result; } Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); while (!queue.isEmpty()) { int levelSize = queue.size(); List<Integer> currentLevel = new ArrayList <>(); for (int i = 0 ; i < levelSize; i++) { TreeNode node = queue.poll(); currentLevel.add(node.val); if (node.left != null ) { queue.offer(node.left); } if (node.right != null ) { queue.offer(node.right); } } result.add(currentLevel); } return result; }
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
1 2 3 4 5 6 7 8 public int maxDepth (TreeNode root) { if (root==null ){ return 0 ; } int left=maxDepth(root.left); int right=maxDepth(root.right); return Math.max(left,right)+1 ; }
给定一个二叉树,判断它是否是高度平衡的二叉树。
1 2 3 4 5 6 7 8 9 public boolean isBalanced (TreeNode root) { if (root == null ) return true ; return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right); } private int depth (TreeNode root) { if (root == null ) return 0 ; return Math.max(depth(root.left), depth(root.right)) + 1 ; }
给你一个二叉树的根节点 root , 检查它是否轴对称。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public boolean isSymmetric (TreeNode root) { if (root == null ) { return true ; } return symmetric(root.left, root.right); } private boolean symmetric (TreeNode left, TreeNode right) { if (left == null && right == null ) { return true ; } if (left == null || right == null || left.val != right.val) { return false ; } return symmetric(left.left, right.right) && symmetric(left.right, right.left); }
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public int diameterOfBinaryTree (TreeNode root) { getHeight(root); return res; } private int getHeight (TreeNode root) { if (root==null ){ return 0 ; } int left=getHeight(root.left); int right=getHeight(root.right); res=Math.max(res,left+right); return Math.max(left,right)+1 ; }
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
1 2 3 4 5 6 7 8 9 public boolean hasPathSum (TreeNode root, int targetSum) { if (root == null ) { return false ; } if (targetSum - root.val == 0 && root.left == null && root.right == null ) { return true ; } return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val); }
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
相当于对每个结点,交换其左右结点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public TreeNode invertTree (TreeNode root) { if (root == null ) { return null ; } Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); while (!queue.isEmpty()) { TreeNode node = queue.poll(); if (node.left != null ) { queue.offer(node.left); } if (node.right != null ) { queue.offer(node.right); } TreeNode temp = node.left; node.left = node.right; node.right = temp; } return root; }
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public boolean isSubtree (TreeNode root, TreeNode subRoot) { if (root == null ) { return false ; } return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot)||dfs(root,subRoot); } private boolean dfs (TreeNode root, TreeNode subRoot) { if (subRoot==null &&root==null ){ return true ; } if (root==null ||subRoot==null ||subRoot.val!=root.val){ return false ; } return dfs(root.left,subRoot.left)&&dfs(root.right,subRoot.right); }
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public List<List<Integer>> binaryTreePaths (TreeNode root) { List<List<Integer>> paths = new ArrayList <>(); if (root == null ) { return paths; } List<Integer> list = new ArrayList <>(); backTrack(root, paths, list); return paths; } private void backTrack (TreeNode root, List<List<Integer>> path, List<Integer> list) { if (root == null ) { return ; } list.add(root.val); if (root.left == null && root.right == null ) { path.add(new ArrayList <>(list)); } else { backTrack(root.left, path, list); backTrack(root.right, path, list); } list.remove(list.size() - 1 ); }
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public List<Integer> rightSideView (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ) { return result; } Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); while (!queue.isEmpty()) { int size = queue.size(); for (int i = 0 ; i < size; i++) { TreeNode node = queue.poll(); if (node.left != null ) { queue.add(node.left); } if (node.right != null ) { queue.add(node.right); } if (i == size - 1 ) { result.add(node.val); } } } return result; }
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 long pre = Long.MIN_VALUE;public boolean isValidBST (TreeNode root) { if (root == null ) { return true ; } if (!isValidBST(root.left)) { return false ; } if (root.val <= pre) { return false ; } pre = root.val; return isValidBST(root.right); }
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
1 2 3 4 5 6 7 8 9 10 11 12 public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { while (root!=null ){ if (p.val<root.val&&q.val<root.val){ root=root.left; }else if (p.val>root.val&&q.val>root.val){ root=root.right; }else { return root; } } return root; }
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
1 2 3 4 5 6 7 8 public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q) return root; TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if (left == null ) return right; if (right == null ) return left; return root; }
请实现两个函数,分别用来序列化和反序列化二叉树,不对序列化之后的字符串进行约束,但要求能够根据序列化之后的字符串重新构造出一棵与原二叉树相同的树。
二叉树的序列化(Serialize)是指:把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串。
二叉树的反序列化(Deserialize)是指:根据某种遍历顺序得到的序列化字符串结果str,重构二叉树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 int index=-1 ;String Serialize (TreeNode root) { if (root==null ){ return "#" ; }else { return root.val+"," +Serialize(root.left)+"," +Serialize(root.right); } } TreeNode Deserialize (String str) { String[] s=str.split("," ); index++; int len=s.length; if (index>len){ return null ; } TreeNode node=null ; if (!s[index].equals("#" )){ node=new TreeNode (Integer.parseInt(s[index])); node.left=Deserialize(str); node.right=Deserialize(str); } return node; }
17、构造二叉树 (1)从前序与中序遍历序列构造二叉树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public TreeNode buildTree (int [] preorder, int [] inorder) { HashMap<Integer, Integer> map = new HashMap <>(); for (int i = 0 ; i < inorder.length; i++) { map.put(inorder[i], i); } return buildTreeHelper(preorder, 0 , preorder.length, inorder, 0 , inorder.length, map); } private TreeNode buildTreeHelper (int [] preorder, int preStart, int preEnd, int [] inorder, int inStart, int inEnd, HashMap<Integer, Integer> map) { if (preStart > preEnd || inStart > inEnd) { return null ; } int rootVal = preorder[preStart]; TreeNode root = new TreeNode (rootVal); int rootIndex = map.get(rootVal); int leftSize = rootIndex - inStart; root.left = buildTreeHelper(preorder, preStart + 1 , preStart + leftSize, inorder, inStart, rootIndex - 1 , map); root.right = buildTreeHelper(preorder, preStart + leftSize + 1 , preEnd, inorder, rootIndex + 1 , inEnd, map); return root; }
(2)从后序与中序遍历序列构造二叉树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public TreeNode buildTree (int [] inorder, int [] postorder) { HashMap<Integer,Integer> map=new HashMap <>(); for (int i=0 ;i<inorder.length;i++){ map.put(inorder[i],i); } return buildTreeHelper(inorder,0 ,inorder.length-1 ,postorder,0 ,postorder.length-1 ,map); } public TreeNode buildTreeHelper (int [] inorder,int i_start,int i_end,int [] postorder,int p_start,int p_end,HashMap<Integer,Integer> map) { if (p_start>p_end||i_start>i_end){ return null ; } int root_val=postorder[p_end]; TreeNode root=new TreeNode (root_val); int i_root_index=map.get(root_val); int leftnum=i_root_index-i_start; root.left=buildTreeHelper(inorder,i_start,i_root_index-1 ,postorder,p_start,p_start+leftnum-1 ,map); root.right=buildTreeHelper(inorder,i_root_index+1 ,i_end,postorder,p_start+leftnum,p_end-1 ,map); return root; }
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public TreeNode sortedArrayToBST (int [] nums) { if (nums == null || nums.length == 0 ) { return null ; } return dfs(nums, 0 , nums.length - 1 ); } private TreeNode dfs (int [] nums, int i, int j) { if (i > j) { return null ; } int mid = i + (j - i) / 2 ; TreeNode root = new TreeNode (nums[mid]); root.left = dfs(nums, i, mid - 1 ); root.right = dfs(nums, mid + 1 , j); return root; }
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int sumNumbers (TreeNode root) { return dfs(root, 0 ); } private int dfs (TreeNode node, int sum) { if (node == null ) { return 0 ; } int currentSum = sum * 10 + node.val; if (node.left == null && node.right == null ) { return currentSum; } int leftSum = dfs(node.left, currentSum); int rightSum = dfs(node.right, currentSum); return leftSum + rightSum; }
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public List<List<Integer>> pathSum (TreeNode root, int targetSum) { List<List<Integer>> res = new ArrayList <>(); List<Integer> list = new ArrayList <>(); backtrack(res, list, root, targetSum); return res; } private void backtrack (List<List<Integer>> res, List<Integer> list, TreeNode root, int targetSum) { if (root == null ) { return ; } list.add(root.val); targetSum -= root.val; if (targetSum == 0 && root.left == null && root.right == null ) { res.add(new ArrayList <>(list)); } backtrack(res, list, root.left, targetSum); backtrack(res, list, root.right, targetSum); list.remove(list.size() - 1 ); }
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public int numTrees (int n) { int [] dp = new int [n + 1 ]; dp[0 ] = 1 ; dp[1 ] = 1 ; for (int i = 2 ; i <= n; i++) { for (int j = 1 ; j <= i; j++) { dp[i] += dp[j - 1 ] * dp[i - j]; } } return dp[n]; }
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(从 1 开始计数)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int kthSmallest (TreeNode root, int k) { Stack<TreeNode> stack = new Stack <>(); int count = 0 ; while (root != null || !stack.isEmpty()) { while (root != null ) { stack.push(root); root = root.left; } root = stack.pop(); count++; if (count == k) { return root.val; } root = root.right; } return -1 ; }
六、贪心算法 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
1 2 3 4 5 6 7 8 public int maxProfit (int [] prices) { int cost = prices[0 ], profit = 0 ; for (int price : prices) { cost = Math.min(cost, price); profit = Math.max(profit, price - cost); } return profit; }
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。返回 你能获得的 最大 利润。
1 2 3 4 5 6 7 8 9 10 public int maxProfit (int [] prices) { int profit = 0 ; for (int i = 1 ; i < prices.length; i++) { int temp = prices[i] - prices[i - 1 ]; if (temp > 0 ) { profit += temp; } } return profit; }
七、动态规划 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
1 2 3 4 5 6 7 8 9 public int climbStairs (int n) { int [] dp=new int [n+1 ]; dp[0 ]=1 ; dp[1 ]=1 ; for (int i=2 ;i<=n;i++){ dp[i]=dp[i-1 ]+dp[i-2 ]; } return dp[n]; }
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
思路:动态规划,初始化dp数组默认值1。
(1)双层遍历,i从1到nums.length,j从0到i,如果nums[j] < nums[i],更新dp[i] = Math.max(dp[i], dp[j] + 1)
(2)外层循环更新maxLen = Math.max(maxLen, dp[i])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int lengthOfLIS (int [] nums) { if (nums == null || nums.length == 0 ) { return 0 ; } int [] dp = new int [nums.length]; dp[0 ] = 1 ; Arrays.fill(dp, 1 ); int maxLen = 1 ; for (int i = 1 ; i < nums.length; i++) { for (int j = 0 ; j < i; j++) { if (nums[j] < nums[i]) { dp[i] = Math.max(dp[i], dp[j] + 1 ); } } maxLen = Math.max(maxLen, dp[i]); } return maxLen; }
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int longestCommonSubsequence (String text1, String text2) { int m = text1.length(), n = text2.length(); int [][] dp = new int [m + 1 ][n + 1 ]; for (int i = 1 ; i <= m; i++) { for (int j = 1 ; j <= n; j++) { char c1 = text1.charAt(i-1 ); char c2 = text2.charAt(j-1 ); if (c1 == c2) { dp[i][j] = dp[i - 1 ][j - 1 ] + 1 ; } else { dp[i][j] = Math.max(dp[i - 1 ][j], dp[i][j - 1 ]); } } } return dp[m][n]; }
(1)一排
1 2 3 4 5 6 7 8 9 10 11 12 13 public int rob (int [] nums) { if (nums == null || nums.length == 0 ) return 0 ; if (nums.length == 1 ) return nums[0 ]; int [] dp = new int [nums.length]; dp[0 ] = nums[0 ]; dp[1 ] = Math.max(dp[0 ], nums[1 ]); for (int i = 2 ; i < nums.length; i++) { dp[i] = Math.max(dp[i - 1 ], dp[i - 2 ] + nums[i]); } return dp[nums.length - 1 ]; }
(2)圆圈
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int rob (int [] nums) { if (nums == null || nums.length == 0 ) { return 0 ; } if (nums.length == 1 ) { return nums[0 ]; } int max1 = robRange(nums, 0 , nums.length - 2 ); int max2 = robRange(nums, 1 , nums.length - 1 ); return Math.max(max1, max2); } private int robRange (int [] nums, int start, int end) { int prevMax = 0 ; int currMax = 0 ; for (int i = start; i <= end; i++) { int temp = currMax; currMax = Math.max(prevMax + nums[i], currMax); prevMax = temp; } return currMax; }
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明: 每次只能向下或者向右移动一步。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int minPathSum (int [][] grid) { if (grid == null || grid.length == 0 ) { return 0 ; } int m = grid.length, n = grid[0 ].length; int [][] dp = new int [m][n]; dp[0 ][0 ] = grid[0 ][0 ]; for (int i = 1 ; i < m; i++) { dp[i][0 ] = dp[i - 1 ][0 ] + grid[i][0 ]; } for (int j = 1 ; j < n; j++) { dp[0 ][j] = dp[0 ][j - 1 ] + grid[0 ][j]; } for (int i = 1 ; i < m; i++) { for (int j = 1 ; j < n; j++) { dp[i][j] = Math.min(dp[i - 1 ][j], dp[i][j - 1 ]) + grid[i][j]; } } return dp[m - 1 ][n - 1 ]; }
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int maximalSquare (char [][] matrix) { int row = matrix.length, col = matrix[0 ].length; if (matrix == null || row == 0 || col == 0 ) { return 0 ; } int [][] dp = new int [row][col]; int maxSide = 0 ; for (int i = 0 ; i < row; i++) { for (int j = 0 ; j < col; j++) { if (matrix[i][j] == '1' ) { if (i == 0 || j == 0 ) { dp[i][j] = 1 ; } else { dp[i][j] = Math.min(Math.min(dp[i - 1 ][j], dp[i][j - 1 ]), dp[i - 1 ][j - 1 ]) + 1 ; } maxSide = Math.max(maxSide, dp[i][j]); } } } return maxSide * maxSide; }
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
1 2 3 4 5 6 7 8 9 10 11 12 13 public int findLength (int [] nums1, int [] nums2) { int m = nums1.length, n = nums2.length; int [][] dp = new int [m + 1 ][n + 1 ]; int res = 0 ; for (int i = m - 1 ; i >= 0 ; i--) { for (int j = n - 1 ; j >= 0 ; j--) { dp[i][j] = nums1[i] == nums2[j] ? dp[i + 1 ][j + 1 ] + 1 : 0 ; res = Math.max(res, dp[i][j]); } } return res; }
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int coinChange (int [] coins, int amount) { int [] dp=new int [amount+1 ]; Arrays.fill(dp,amount+1 ); dp[0 ]=0 ; for (int i=1 ;i<=amount;i++){ for (int coin:coins){ if (coin<=i){ dp[i]=Math.min(dp[i],dp[i-coin]+1 ); } } } return dp[amount]>amount?-1 :dp[amount]; }
给你一个整数 n ,返回和为 n 的完全平方数的最少数量。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数。
1 2 3 4 5 6 7 8 9 10 11 12 13 public int numSquares (int n) { int dp[] = new int [n + 1 ]; Arrays.fill(dp, Integer.MAX_VALUE); dp[0 ] = 0 ; for (int i = 1 ; i <= n; i++) { for (int j = 1 ; j * j <= i; j++) { dp[i] = Math.min(dp[i], dp[i - j * j] + 1 ); } } return dp[n]; }
八、深度/广度优先遍历 给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int numIslands (char [][] grid) { int count = 0 ; for (int i = 0 ; i < grid.length; i++) { for (int j = 0 ; j < grid[0 ].length; j++) { if (grid[i][j] == '1' ) { dfs(grid, i, j); count++; } } } return count; } private void dfs (char [][] grid, int i, int j) { if (i < 0 || i >= grid.length || j < 0 || j >= grid[0 ].length || grid[i][j] == '0' ) { return ; } grid[i][j] = '0' ; dfs(grid, i + 1 , j); dfs(grid, i, j + 1 ); dfs(grid, i - 1 , j); dfs(grid, i, j - 1 ); }
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public List<String> generateParenthesis (int n) { List<String> res=new ArrayList <>(); dfs(n,n,res,"" ); return res; } private void dfs (int left, int right, List<String> res, String cur) { if (left == 0 && right == 0 ) { res.add(cur); return ; } if (left > 0 ) { dfs(left - 1 , right, res, cur + "(" ); } if (right > left) { dfs(left, right - 1 , res, cur + ")" ); } }
有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
返回既能流向太平洋,也能流向大西洋的数字下标list。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public List<List<Integer>> pacificAndAtlantic (int [][] matrix) { if (matrix==null ||matrix.length==0 ){ return new ArrayList <>(); } int m=matrix.length; int n=matrix[0 ].length; int [][] pacific=new int [m][n]; int [][] atlantic=new int [m][n]; for (int i=0 ;i<m;i++){ for (int j=0 ;j<n;j++){ if (i==0 ||j==0 ){ dfs(matrix,pacific,i,j,matrix[i][j]); } if (i==m-1 ||j==n-1 ){ dfs(matrix,atlantic,i,j,matrix[i][j]); } } } List<List<Integer>> res=new ArrayList <>(); for (int i=0 ;i<m;i++){ for (int j=0 ;j<n;j++){ if (pacific[i][j]==1 &&atlantic[i][j]==1 ){ res.add(Arrays.asList(i,j)); } } } return res; } public void dfs (int [][] matrix,int [][] ocean,int i,int j,int pre) { if (i<0 || i>=matrix.length || j<0 || j>=matrix[0 ].length || ocean[i][j]==1 || matrix[i][j]<pre){ return ; } ocean[i][j]=1 ; dfs(matrix, ocean, i - 1 , j, matrix[i][j]); dfs(matrix, ocean, i + 1 , j, matrix[i][j]); dfs(matrix, ocean, i, j - 1 , matrix[i][j]); dfs(matrix, ocean, i, j + 1 , matrix[i][j]); }
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 public void sounded (char [][] board) { if (board==null ||board.length==0 ){ return ; } int m=board.length; int n=board[0 ].length; for (int i=0 ;i<m;i++){ for (int j=0 ;j<n;j++){ boolean isEdge=(i==0 ||i==m-1 ||j==0 ||j==n-1 ); if (isEdge&&board[i][j]=='O' ){ dfs(board,i,j); } } } for (int i=0 ;i<m;i++){ for (int j=0 ;j<n;j++){ if (board[i][j]=='O' ){ board[i][j]='X' ; } if (board[i][j]=='#' ){ board[i][j]='O' ; } } } } public void dfs (char [][] board,int i,int j) { if (i < 0 || j < 0 || i >= board.length || j >= board[0 ].length || board[i][j] == 'X' || board[i][j] == '#' ){ return ; } board[i][j]='#' ; dfs(board,i+1 ,j); dfs(board,i-1 ,j); dfs(board,i,j+1 ); dfs(board,i,j-1 ); }
九、回溯算法 (1)给定一个不含重复数字 的数组 nums ,返回其 所有可能的全排列。你可以 按任意顺序 返回答案。
思路:回溯
(1)list的大小和nums数组长度相同时,加入list到结果集res。
(2)for循环遍历数组,如果list存在nums[i],跳过该数,并进行常规添加-回溯下一层-撤销操作。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public List<List<Integer>> permute (int [] nums) { List<List<Integer>> res = new ArrayList <>(); List<Integer> list = new ArrayList <>(); backTrack(nums, res, list); return res; } private void backTrack (int [] nums, List<List<Integer>> res, List<Integer> list) { if (list.size() == nums.length) { res.add(new ArrayList <>(list)); } for (int i = 0 ; i < nums.length; i++) { if (list.contains(nums[i])){ continue ; } list.add(nums[i]); backTrack(nums, res, list); list.remove(list.size() - 1 ); } }
(2)给定一个可包含重复数字 的序列 nums ,按任意顺序 返回所有不重复的全排列。
思路:由于存在重复元素,添加boolean[] used数组记录当前数字是否用过。
(1)为方便去重,先对nums进行排序。
(2)在数组循环中,跳过重复元素或已使用的元素
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public List<List<Integer>> permuteUnique (int [] nums) { List<List<Integer>> res = new ArrayList <>(); List<Integer> list = new ArrayList <>(); boolean [] used = new boolean [nums.length]; Arrays.sort(nums); backtrack(res, list, nums, used); return res; } private void backtrack (List<List<Integer>> res, List<Integer> list, int [] nums, boolean [] used) { if (list.size() == nums.length) { res.add(new ArrayList <>(list)); return ; } for (int i = 0 ; i < nums.length; i++) { if (used[i] || (i > 0 && nums[i] == nums[i - 1 ] && !used[i - 1 ])) { continue ; } used[i] = true ; list.add(nums[i]); backtrack(res, list, nums, used); used[i] = false ; list.remove(list.size() - 1 ); } }
(1)给定一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public List<List<Integer>> subsets (int [] nums) { List<List<Integer>> result = new ArrayList <>(); List<Integer> currentSubset = new ArrayList <>(); backtrack(nums, 0 , currentSubset, result); return result; } private void backtrack (int [] nums, int start, List<Integer> currentSubset, List<List<Integer>> result) { result.add(new ArrayList <>(currentSubset)); for (int i = start; i < nums.length; i++) { currentSubset.add(nums[i]); backtrack(nums, i + 1 , currentSubset, result); currentSubset.remove(currentSubset.size() - 1 ); } }
(2)给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public List<List<Integer>> subsetsWithDup (int [] nums) { List<List<Integer>> result = new ArrayList <>(); Arrays.sort(nums); backtrack(nums, 0 , new ArrayList <>(), result); return result; } private void backtrack (int [] nums, int start, List<Integer> currentSubset, List<List<Integer>> result) { result.add(new ArrayList <>(currentSubset)); for (int i = start; i < nums.length; i++) { if (i > start && nums[i] == nums[i - 1 ]) { continue ; } currentSubset.add(nums[i]); backtrack(nums, i + 1 , currentSubset, result); currentSubset.remove(currentSubset.size() - 1 ); } }
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public boolean exist (char [][] board, String word) { if (board == null || board.length == 0 || word == null || word.length() == 0 ) { return false ; } int rows = board.length; int cols = board[0 ].length; boolean [][] visited = new boolean [rows][cols]; for (int i = 0 ; i < rows; i++) { for (int j = 0 ; j < cols; j++) { if (board[i][j] == word.charAt(0 ) && backtrack(board, word, i, j, 0 , visited)) { return true ; } } } return false ; } private boolean backtrack (char [][] board, String word, int row, int col, int index, boolean [][] visited) { if (index == word.length()) { return true ; } if (row < 0 || col < 0 || row >= board.length || col >= board[0 ].length || visited[row][col] || board[row][col] != word.charAt(index)) { return false ; } visited[row][col] = true ; boolean result = backtrack(board, word, row + 1 , col, index + 1 , visited) || backtrack(board, word, row - 1 , col, index + 1 , visited) || backtrack(board, word, row, col + 1 , index + 1 , visited) || backtrack(board, word, row, col - 1 , index + 1 , visited); visited[row][col] = false ; return result; }
4、组合 (1)给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 。
candidates 中的 同一个 数字可以 无限制重复被选取 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public List<List<Integer>> combinationSum (int [] candidates, int target) { List<List<Integer>> combinations=new ArrayList <>(); List<Integer> res=new ArrayList <>(); backtrack(combinations,res,candidates,target,0 ); return combinations; } private void backtrack (List<List<Integer>> combinations,List<Integer> res,int [] candidates,int target,int start) { if (target==0 ){ combinations.add(new ArrayList <>(res)); return ; } for (int i=start;i<candidates.length;i++){ if (candidates[i]<=target){ res.add(candidates[i]); backtrack(combinations,res,candidates,target-candidates[i],i); res.remove(res.size()-1 ); } } }
(2)给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public List<List<Integer>> combine (int n, int k) { List<List<Integer>> result = new ArrayList <>(); List<Integer> current = new ArrayList <>(); backtrack(result, current, n, k, 1 ); return result; } private void backtrack (List<List<Integer>> result, List<Integer> current, int n, int k, int start) { if (k == 0 ) { result.add(new ArrayList <>(current)); return ; } for (int i = start; i <= n; i++) { current.add(i); backtrack(result, current, n, k - 1 , i + 1 ); current.remove(current.size() - 1 ); } }
给定一个字符串 s ,请将 s 分割成一些子串,使每个子串都是 回文串 ,返回 s 所有可能的分割方案。
示例 1:
1 2 输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public List<List<String>> partition (String s) { List<List<String>> partitions=new ArrayList <>(); List<String> curpartion=new ArrayList <>(); doPartition(s,partitions,curpartion); return partitions; } private void doPartition (String s,List<List<String>> partitions,List<String> curpartion) { if (s.length()==0 ){ partitions.add(new ArrayList <>(curpartion)); return ; } for (int i=0 ;i<s.length();i++){ if (isPalindrome(s,0 ,i)){ curpartion.add(s.substring(0 ,i+1 )); doPartition(s.substring(i+1 ),partitions,curpartion); curpartion.remove(curpartion.size()-1 ); } } } private boolean isPalindrome (String s,int i,int j) { while (i<j){ if (s.charAt(i++)!=s.charAt(j--)){ return false ; } } return true ; }
6、复原IP地址 给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址 。有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public List<String> restoreIpAddresses (String s) { List<String> result = new ArrayList <>(); if (s.length() < 4 || s.length() > 12 ) { return result; } backtrack(s, 0 , 0 , "" , result); return result; } private void backtrack (String s, int start, int segmentId, String currentIp, List<String> result) { if (segmentId == 4 && start == s.length()) { result.add(currentIp.substring(0 , currentIp.length() - 1 )); return ; } if (segmentId == 4 ) { return ; } for (int end = start; end < Math.min(start + 3 , s.length()); end++) { String segment = s.substring(start, end + 1 ); if (isValid(segment)) { backtrack(s, end + 1 , segmentId + 1 , currentIp + segment + "." , result); } } } private boolean isValid (String segment) { if (segment.startsWith("0" ) && segment.length() > 1 ) { return false ; } int num = Integer.parseInt(segment); return num >= 0 && num <= 255 ; }
十、多线程 1、线程a、b、c顺序执行 要求线程a执行完才开始线程b,线程b执行完才开始线程c。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 public class ThreadExecutionOrder { public static void main (String[] args) { Thread threadA = new Thread (new Task ("Thread A" )); Thread threadB = new Thread (new Task ("Thread B" )); Thread threadC = new Thread (new Task ("Thread C" )); try { threadA.start(); threadA.join(); threadB.start(); threadB.join(); threadC.start(); threadC.join(); } catch (InterruptedException e) { e.printStackTrace(); } } static class Task implements Runnable { private final String name; public Task (String name) { this .name = name; } @Override public void run () { System.out.println(name + " is running." ); System.out.println(name + " is done." ); } } }
2、两个线程轮流打印数字 两个线程轮流打印数字,从1到100。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public class PrintNumbers { private static final int MAX_NUMBER = 100 ; private static int number = 1 ; private static final Object lock = new Object (); public static void main (String[] args) { Thread thread1 = new Thread (new PrintNumberTask (1 )); Thread thread2 = new Thread (new PrintNumberTask (2 )); thread1.start(); thread2.start(); } static class PrintNumberTask implements Runnable { private final int threadId; public PrintNumberTask (int threadId) { this .threadId = threadId; } @Override public void run () { while (number <= MAX_NUMBER) { synchronized (lock) { if (number % 2 == threadId - 1 ) { System.out.println("Thread " + threadId + ": " + number); number++; lock.notifyAll(); } else { try { lock.wait(); } catch (InterruptedException e) { e.printStackTrace(); } } } } } } }
解释:
判断 number % 2 == threadId - 1 的目的是为了确定当前线程是否应该打印当前的数字。
在这里, number 表示当前要打印的数字, threadId 表示线程的ID(1或2)。根据这个判断条件,两个线程将交替打印数字。
具体解释如下:
当 threadId 为1时,判断条件为 number % 2 == 0 。这意味着只有当 number 为偶数时,线程1才会打印该数字。
当 threadId 为2时,判断条件为 number % 2 == 1 。这意味着只有当 number 为奇数时,线程2才会打印该数字。
通过这种方式,两个线程在获取到锁后会进行条件判断,只有符合条件的线程才会执行打印操作,并将 number 加1。否则,线程会通过 wait() 方法释放锁并等待,直到被其他线程通过 notifyAll() 方法唤醒。
3、两个线程按序轮流打印 写两个线程,一个线程打印1~ 52,另一个线程打印A~Z,打印顺序是12A34B…5152Z。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 public class PrintNumbersAndLetters { private static final Object lock = new Object (); private static int number = 1 ; private static char letter = 'A' ; public static void main (String[] args) { Thread numberThread = new Thread (new PrintNumberTask ()); Thread letterThread = new Thread (new PrintLetterTask ()); numberThread.start(); letterThread.start(); } static class PrintNumberTask implements Runnable { @Override public void run () { synchronized (lock) { while (number <= 52 ) { if (number % 2 == 1 ) { System.out.print(number); number++; System.out.print(number); number++; lock.notify(); } else { try { lock.wait(); } catch (InterruptedException e) { e.printStackTrace(); } } } } } } static class PrintLetterTask implements Runnable { @Override public void run () { synchronized (lock) { while (letter <= 'Z' ) { System.out.print(letter); letter++; lock.notify(); try { lock.wait(); } catch (InterruptedException e) { e.printStackTrace(); } } } } } }
解释:
在 PrintNumberTask 中,使用 while 循环判断 number 是否小于等于52。如果是奇数,则打印当前数字和下一个数字,并将 number 加2。然后通过 notify() 方法唤醒等待的线程,并自己进入等待状态。如果是偶数,则通过 wait() 方法释放锁并等待。
在 PrintLetterTask 中,使用 while 循环判断 letter 是否小于等于字母’Z’。每次循环打印当前字母,并将 letter 递增。然后通过 notify() 方法唤醒等待的线程,并自己进入等待状态。
4、三个线程按次序轮流打印 编写一个程序,启动三个线程,三个线程的ID分别是A,B,C;,每个线程将自己的ID值在屏幕上打印5遍,打印顺序是ABCABC…
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public class PrintABC { private static final Object lock = new Object (); private static int currentThread = 0 ; private static final int MAX_COUNT = 5 ; public static void main (String[] args) { Thread threadA = new Thread (new PrintTask ("A" , 0 )); Thread threadB = new Thread (new PrintTask ("B" , 1 )); Thread threadC = new Thread (new PrintTask ("C" , 2 )); threadA.start(); threadB.start(); threadC.start(); } static class PrintTask implements Runnable { private final String threadId; private final int id; public PrintTask (String threadId, int id) { this .threadId = threadId; this .id = id; } @Override public void run () { for (int i = 0 ; i < MAX_COUNT; i++) { synchronized (lock) { while (currentThread != id) { try { lock.wait(); } catch (InterruptedException e) { e.printStackTrace(); } } System.out.print(threadId); currentThread = (currentThread + 1 ) % 3 ; lock.notifyAll(); } } } } }
解释:
在 PrintTask 中,使用 for 循环来打印ID值。在每次循环中,线程首先通过 synchronized 块获取到锁,并检查 currentThread 的值是否等于自己的ID值。如果不是,则线程进入等待状态,释放锁并等待被唤醒。如果是,则打印自己的ID值,并更新 currentThread 的值为下一个线程的ID。最后,通过 notifyAll() 方法唤醒其他等待的线程,并释放锁。
5、十个线程打印求和 编写10个线程,第一个线程从1加到10,第二个线程从11加20…第十个线程从91加到100,最后再把10个线程结果相加。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public class TenThreadSum { public static class SumThread extends Thread { int forct = 0 ; int sum = 0 ; SumThread(int forct){ this .forct = forct; } @Override public void run () { for (int i = 1 ; i <= 10 ; i++){ sum += i + forct * 10 ; } System.out.println(getName() + " " + sum); } } public static void main (String[] args) { int result = 0 ; for (int i = 0 ; i < 10 ; i++){ SumThread sumThread = new SumThread (i); sumThread.start(); try { sumThread.join(); } catch (InterruptedException e) { e.printStackTrace(); } result = result + sumThread.sum; } System.out.println("result " + result); } }
6、三个窗口同时卖票 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 public class TicketSeller { private static int tickets = 100 ; public static void main (String[] args) { Thread seller1 = new Thread (new Seller (), "窗口1" ); Thread seller2 = new Thread (new Seller (), "窗口2" ); Thread seller3 = new Thread (new Seller (), "窗口3" ); seller1.start(); seller2.start(); seller3.start(); } static class Seller implements Runnable { @Override public void run () { while (true ) { synchronized (TicketSeller.class) { if (tickets > 0 ) { System.out.println(Thread.currentThread().getName() + "售出票号:" + tickets); tickets--; } else { break ; } } } } } }
7、交替打印两个数组 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public class AlternatePrint { private static final Object lock = new Object (); private static boolean printFirstArray = true ; public static void main (String[] args) { int [] array1 = {1 , 3 , 5 , 7 , 9 }; int [] array2 = {2 , 4 , 6 , 8 , 10 }; Thread thread1 = new Thread (new PrintTask (array1)); Thread thread2 = new Thread (new PrintTask (array2)); thread1.start(); thread2.start(); } static class PrintTask implements Runnable { private final int [] array; public PrintTask (int [] array) { this .array = array; } @Override public void run () { for (int num : array) { synchronized (lock) { while ((printFirstArray && array != array1) || (!printFirstArray && array != array2)) { try { lock.wait(); } catch (InterruptedException e) { e.printStackTrace(); } } System.out.println(num); printFirstArray = !printFirstArray; lock.notifyAll(); } } } } }
解释:
我们创建了两个线程 thread1 和 thread2 ,它们分别负责打印 array1 和 array2 的元素。每个线程通过循环遍历数组,并使用 synchronized 关键字获取到共享的锁对象 lock 。
在每次循环中,线程首先通过 synchronized 块获取到锁,并检查当前应该打印的数组是否与自己负责打印的数组相符。如果不相符,则线程进入等待状态,释放锁并等待被唤醒。如果相符,则打印当前元素,并将 printFirstArray 的值取反,以便下一个线程可以打印另一个数组的元素。最后,通过 notifyAll() 方法唤醒其他等待的线程,并释放锁。
8、生产者消费者模式 1、BlockingQueue 实现生产者消费者模式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public static void main (String[] args) { BlockingQueue<Object> queue=new ArrayBlockingQueue <>(10 ); Runnable producer=()->{ while (true ){ try { queue.put(new Object ()); System.out.println("producing..." ); } catch (InterruptedException e) { throw new RuntimeException (e); } } }; new Thread (producer).start(); Runnable consumer=()->{ while (true ){ try { queue.take(); System.out.println("taking..." ); } catch (InterruptedException e) { throw new RuntimeException (e); } } }; new Thread (consumer).start(); }
2、Condition 实现生产者消费者模式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 private Queue queue; private int size; private ReentrantLock lock=new ReentrantLock (); private Condition notFull=lock.newCondition(); private Condition notEmpty=lock.newCondition(); public ProducerAndConsumerMode (int size) { this .size=size; queue=new LinkedList (); } public void put (Object o) throws InterruptedException{ lock.lock(); try { while (queue.size()==size){ notFull.await(); } queue.add(o); notEmpty.signalAll(); }finally { lock.unlock(); } } public void take (Object o) throws InterruptedException{ lock.lock(); try { while (queue.size()==0 ){ notEmpty.await(); } queue.remove(o); notFull.signalAll(); }finally { lock.unlock(); } }
3、wait/notify方法实现生产者消费者
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 private int maxSize; private LinkedList<Object> storage=new LinkedList <>(); public ProducerAndConsumerMode (int size, LinkedList<Object> storage) { this .maxSize = size; this .storage = storage; } public synchronized void put () throws InterruptedException { while (storage.size() == maxSize) { wait(); } storage.add(new Object ()); notifyAll(); } public synchronized void take () throws InterruptedException { while (storage.size() == 0 ) { wait(); } System.out.println(storage.remove()); notifyAll(); }